Com a mecanisme de transmissió, l'engranatge planetari s'utilitza àmpliament en diverses pràctiques d'enginyeria, com ara reductors d'engranatges, grues, reductors d'engranatges planetaris, etc. Per als reductors d'engranatges planetaris, poden substituir el mecanisme de transmissió del tren d'engranatges d'eix fix en molts casos. Com que el procés de transmissió d'engranatges és per contacte lineal, l'engranament a llarg termini provocarà una fallada de l'engranatge, per la qual cosa cal simular la seva resistència. Li Hongli et al. van utilitzar el mètode d'engranament automàtic per mallar l'engranatge planetari i van obtenir que el parell i la tensió màxima són lineals. Wang Yanjun et al. també van mallar l'engranatge planetari mitjançant el mètode de generació automàtica i van simular la simulació estàtica i modal de l'engranatge planetari. En aquest article, els elements de tetraedre i hexaedre s'utilitzen principalment per dividir la malla, i els resultats finals s'analitzen per veure si es compleixen les condicions de resistència.

1. Establiment del model i anàlisi de resultats

Modelatge tridimensional d'engranatges planetaris

engranatge planetariestà compost principalment per una corona d'engranatge, un engranatge solar i un engranatge planetari. Els paràmetres principals seleccionats en aquest article són: el nombre de dents de l'anell d'engranatge interior és de 66, el nombre de dents de l'engranatge solar és de 36, el nombre de dents de l'engranatge planetari és de 15, el diàmetre exterior de l'anell d'engranatge interior és de 150 mm, el mòdul és de 2 mm, l'angle de pressió és de 20 °, l'amplada de la dent és de 20 mm, el coeficient d'alçada de l'afegit és d'1, el coeficient de joc és de 0,25 i hi ha tres engranatges planetaris.

Anàlisi de simulació estàtica d'engranatges planetaris

Definiu les propietats del material: importeu el sistema d'engranatges planetaris tridimensional dibuixat amb el programari UG a ANSYS i configureu els paràmetres del material, tal com es mostra a la Taula 1 següent:

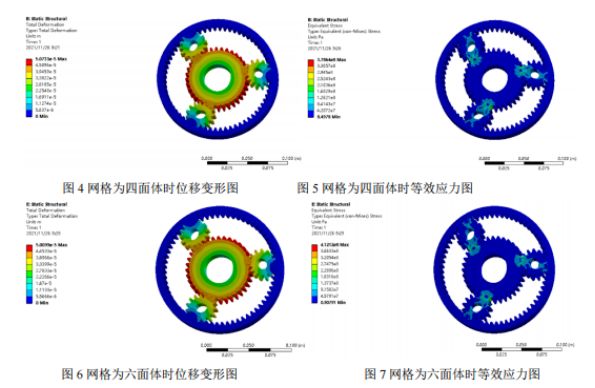
Malla: La malla d'elements finits es divideix per tetraedre i hexaedre, i la mida bàsica de l'element és de 5 mm. Com queengranatge planetari, l'engranatge solar i l'anell de l'engranatge interior estan en contacte i engranant, la malla de les parts de contacte i de malla es densifica i la mida és de 2 mm. Primer, s'utilitzen malles tetraèdriques, com es mostra a la Figura 1. Es generen un total de 105906 elements i 177893 nodes. A continuació, s'adopta la malla hexaèdrica, com es mostra a la Figura 2, i es generen un total de 26957 cel·les i 140560 nodes.

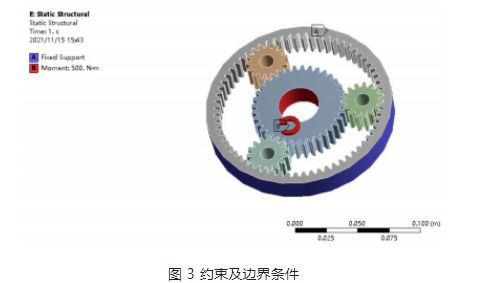
Aplicació de càrrega i condicions de contorn: segons les característiques de treball de l'engranatge planetari del reductor, l'engranatge solar és l'engranatge motriu, l'engranatge planetari és l'engranatge accionat i la sortida final és a través del portaplanetari. Fixeu l'anell de l'engranatge interior a l'ANSYS i apliqueu un parell de 500 N · m a l'engranatge solar, tal com es mostra a la Figura 3.

Postprocessament i anàlisi de resultats: A continuació es mostren el nefograma de desplaçament i el nefograma de tensió equivalent de l'anàlisi estàtica obtinguts a partir de dues divisions de la malla, i es realitza una anàlisi comparativa. A partir del nefograma de desplaçament dels dos tipus de malles, es constata que el desplaçament màxim es produeix a la posició on l'engranatge solar no engrana amb l'engranatge planetari, i la tensió màxima es produeix a l'arrel de l'engranatge de l'engranatge. La tensió màxima de la malla tetraèdrica és de 378 MPa i la tensió màxima de la malla hexaèdrica és de 412 MPa. Com que el límit de fluència del material és de 785 MPa i el factor de seguretat és d'1,5, la tensió admissible és de 523 MPa. La tensió màxima d'ambdós resultats és inferior a la tensió admissible, i tots dos compleixen les condicions de resistència.

2. Conclusió

Mitjançant la simulació d'elements finits de l'engranatge planetari, s'obtenen el nefograma de desplaçament i deformació i el nefograma de tensió equivalent del sistema d'engranatges, dels quals es desprenen les dades màximes i mínimes i la seva distribució en el...engranatge planetaries pot trobar el model. La ubicació de la tensió equivalent màxima també és la ubicació on és més probable que les dents de l'engranatge fallin, per la qual cosa s'hi ha de prestar especial atenció durant el disseny o la fabricació. Mitjançant l'anàlisi de tot el sistema d'engranatges planetaris, es supera l'error causat per l'anàlisi d'una sola dent d'engranatge.